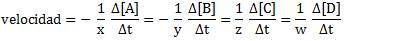Las unidades convencionales de la velocidad (“distancia/tiempo”) nos dicen cuánta distancia recorre un cuerpo en un determinado tiempo. En química estas unidades no nos sirven, ya que los cuerpos, a nivel macroscópico, no se mueven. Sin embargo, usaremos unidades las de “concentración/tiempo”, con el objetivo de expresar el cambio en la concentración de un reactivo o de un producto con respecto al tiempo.

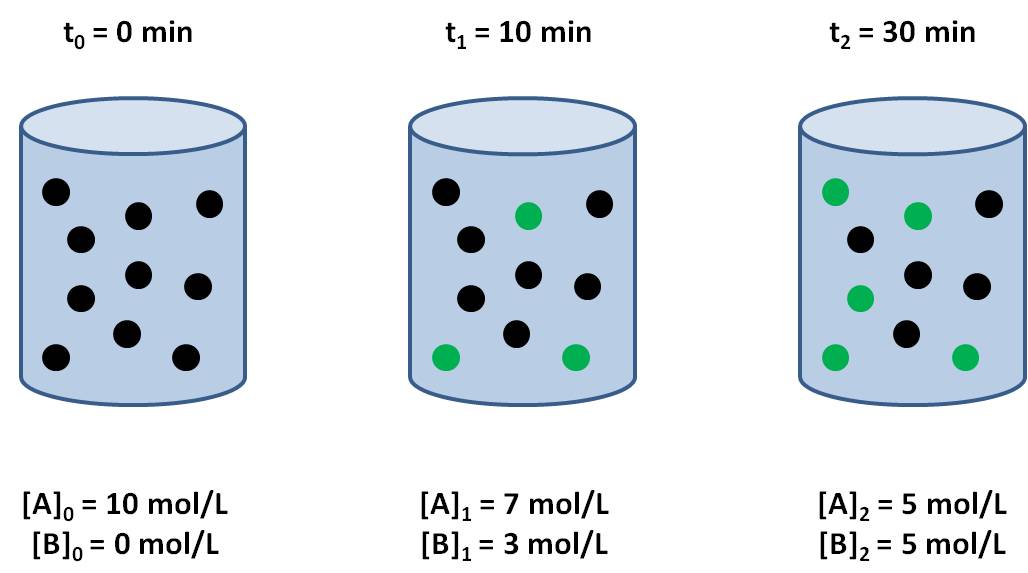
Imaginemos la siguiente reacción, en la que la sustancia A, de color negra, se transforma en B, de color verde, en un recipiente de 1 L:  A → B

Al inicio de la reacción sólo tendremos moles de A. Representemos esto según el gráfico mostrado a continuación. Al inicio (tiempo = 0 segundos), sólo vemos moles de A (esferas de color negro). Sin embargo, transcurrido un intervalo de tiempo (en nuestro ejemplo, 10 minutos) hasta el tiempo t₁, algunas moles de A se han transformado ya en B. Asimismo, el número de moles de B es mayor al tiempo t₂:

Nuestras expresiones de velocidad promedio para la reacción las podemos expresar en función tanto a A como a B:

Las velocidades siempre deben ser positivas, por tanto, observa el signo que se ha colocado delante del a expresión de la velocidad que depende de la concentración de A: la sustancia A es un reactivo, por tanto, su concentración en el tiempo disminuye y el ?[A] es negativo. Para contrarrestar esto y tener expresiones de velocidad positivas, se coloca un signo delante de la velocidad promedio que depende de un reactivo.

Por ejemplo, en el intervalo t₀ – t₁, la velocidad promedio de desaparición de A será:

Δ[A] = 7 mol/L – 10 mol/L = - 3 mol/L
Δt = 10 min – 0 min = 10 min

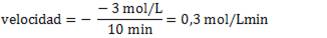
Verifica que la velocidad de aparición de B es la misma en dicho intervalo.

Si graficamos las concentraciones de las sustancias involucradas en la reacción versus el tiempo, obtendríamos un gráfico como el mostrado a continuación:

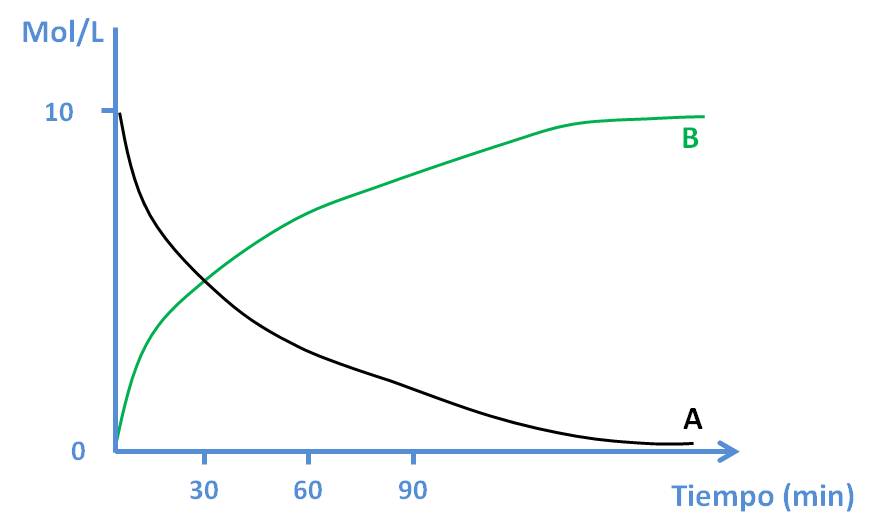
Estos gráficos nos ayudan a entender cómo transcurre la reacción con el tiempo: al inicio de la reacción, sólo tenemos al reactivo A y nada de B. Con el trascurrir del tiempo, la concentración de A va disminuyendo, mientras que la de B va creciendo. Estas variaciones ocurren hasta un cierto punto, donde la velocidad disminuye notablemente hasta que casi no cambia más. Este instante viene dado por el final de la reacción: el momento en que todo el reactivo se transformó en producto. Como verás, la velocidad depende del instante en que analicemos la reacción: está claro que la velocidad al inicio no es la misma que al final.

Al calcular la velocidad promedio de la reacción en intervalos de tiempo más cortos, podemos obtener la velocidad en un determinado instante de la reacción, lo cual proporciona la velocidad instantánea.  La principal diferencia entre estas dos velocidades es que la velocidad promedio se calcula para un intervalo de tiempo, mientras que la velocidad instantánea se determina en un momento dado. En forma gráfica, la velocidad instantánea está dada por la pendiente de la recta tangente a la curva a un determinado tiempo. En forma matemática (y obviando el signo), podemos expresarlas así:

VELOCIDAD DE REACCIÓN Y ESTEQUIOMETRÍA

Analicemos la siguiente reacción de descomposición del diborano (B₂H₆):

B₂H₆ →  2 BH₃

Vemos que se forman dos moles de BH₃ por cada mol de B₂H₆. Eso quiere decir que desaparece una mol de B₂H₆ por cada dos moles de BH₃ que se forman. Entonces, podemos decir que la velocidad de aparición del BH₃ es el doble de rápido que la velocidad de desaparición del B₂H₆. De esta forma, podemos expresar la velocidad de la reacción como:

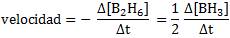
Por tanto, debemos tener en cuenta siempre a los coeficientes estequiométricos, ya que son importantes en la expresión de la velocidad de una reacción.

En general, para la siguiente reacción hipotética balanceada:

x A  +  y B →  z C  +  w D

podemos afirmar que la velocidad está dada por: