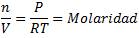Hemos aprendido ya que la velocidad de una reacción depende de la concentración de los reactivos, y que no necesariamente todos los reactivos son importantes en tal velocidad: algunos influyen más que otros. Pero, ¿nos interesa realmente conocer qué tan rápido ocurre una reacción? Lo cierto es que esto sirve sólo si queremos conocer al detalle cómo transcurre una reacción. Pero la principal utilidad de la ley de velocidad es que nos permite calcular la concentración de un reactivo luego de un determinado tiempo. Esto es muy importante, por ejemplo, con las medicinas: el efecto que producen decae con el tiempo, debido a una reacción de descomposición del principio activo. A continuación aprenderemos a calcular la concentración de un reactivo en función a la ley de velocidad. Para ello, debemos conocer el orden de la reacción.

REACCIONES DE ORDEN CERO

Las reacciones de orden cero son aquellas en que la velocidad no depende de la concentración de los reactivos. Por tanto, es constante a lo largo del a reacción.

Para una reacción genérica: A  →  B, la ley de velocidad será: v = k[A]⁰ = k

Recordemos que la velocidad la podemos expresar, también, como la variación de la concentración en función del tiempo, con signo negativo (dado que hablamos de un reactivo). Por tanto:

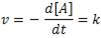
Estamos, por tanto, ante una ecuación diferencial. Si la reescribimos, podemos tener lo siguiente:

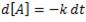
Esta ecuación, ahora, la podemos integrar:

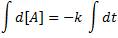
De lo que obtenemos:

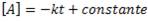
Para determinar el valor de la constante de integración, analicemos qué pasa si t = 0: es el inicio del a reacción, por tanto, la concentración es la inicial de A. Esta concentración la denotaremos con el subíndice cero:

De esta forma, tenemos ya una expresión que nos permite calcular la concentración de del reactivo A luego de un determinado tiempo t. Para poder usar la ecuación, necesitamos saber la concentración inicial de A, y la constante de velocidad (hallada en la ley de velocidad).

¿Qué unidades tendrá k? Pues analicemos la ecuación: las concentraciones siempre están dadas en molaridad, por tanto, por análisis dimensional:

Molaridad = [constante] x tiempo
por tanto:   [constante] = Mt^-1   

Estas son las unidades de la constante de velocidad de una reacción de orden cero: Mt^-1.

Analicemos nuevamente nuestra ecuación:

Esta ecuación se asemeja a la de una recta: si consideramos que la concentración de A (eje “y”) está variando en el tiempo (eje “x”), la pendiente de tal recta será la constante de velocidad. Tal pendiente, debido al signo, será negativa. Y el punto de corte de la recta con el eje “y” coincidirá con el valor de la concentración de A inicial. En forma gráfica:

Observación Recuerda que debemos expresar la concentración molar para poder utilizar estas ecuaciones. Las únicas especies que pueden tener concentración molar son las SOLUCIONES y los GASES. De la ecuación del gas ideal podemos deducir lo siguiente: Por tanto, conociendo la presión parcial de un gas y la temperatura a la que se encuentra, podemos estimar su molaridad. Si trabajamos con sólidos y líquidos, no podemos usar la ley de velocidad: debemos usar los datos de alguna especie gaseosa o acuosa que se encuentre en la misma reacción.

Ejemplo 2.1. El amoníaco se descompone sobre superficies de tungsteno a 900°C en nitrógeno e hidrógeno, según la siguiente reacción: 2 NH3(g) →   N2(g)  +  3 H2(g) A esa temperatura, la constante de velocidad es de 1,67x10-4 M/min. Determinar cuánto tiempo tardará en descomponerse totalmente el amoníaco, si la presión inicial de éste es de 2 atm.

Analicemos las unidades de la constante: molaridad / tiempo. Corresponden a las unidades de una constante de velocidad de orden cero. Por tanto, se cumplirá que:

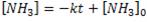
Queremos conocer cuánto tiempo transcurre hasta que la [NH₃]=0. Para ello, necesitamos conocer la concentración inicial de amoníaco. Como es un gas, su molaridad vendrá dada por:

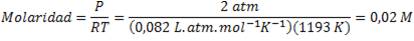
Entonces, en nuestra ecuación:

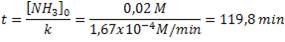
Por tanto, el tiempo necesario para que se consuma totalmente el amoníaco será de 119,8 minutos (casi dos horas).

REACCIONES DE PRIMER ORDEN

Para una reacción genérica de primer orden:    A → B,  la ley de velocidad será: v = k[A]¹

o, lo que es lo mismo:

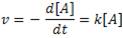
Resolviendo esta ecuación diferencial, llegamos a la expresión:

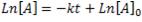
y las unidades de la constante de velocidad, en el caso de reacciones de primer orden, es: t^-1

En este caso, obtenemos también una recta al relacionar las concentraciones y el tiempo. El único cuidado es que debemos graficar el logaritmo natural de la concentración vs el tiempo. Así:

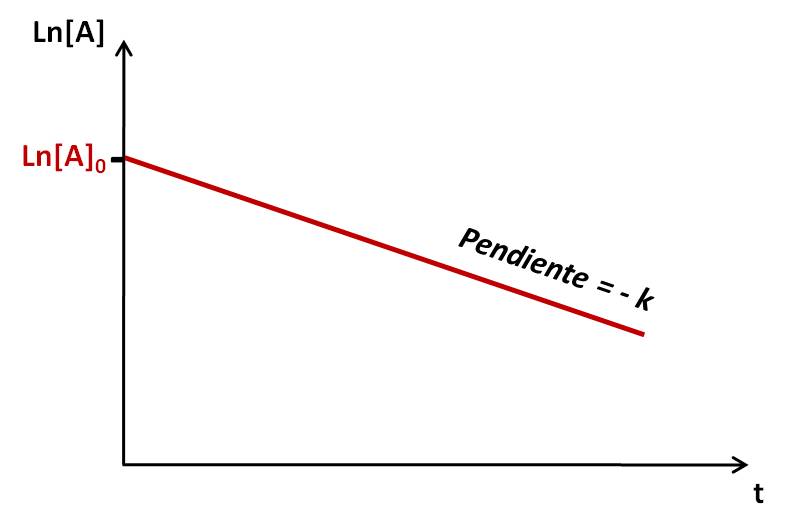
Ejemplo 2.2. Al cabo de 35 minutos en una reacción de primer orden, ha reaccionado sólo el 30% del reactivo. Determinar: La constante de velocidad. El porcentaje del reactivo que queda luego de 4 horas.

Es una reacción de primer orden, se cumple entonces:

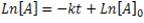
Si ha reaccionado el 30% del reactivo, quiere decir que queda un 70% del mismo. Entonces, podemos decir que después de 35 minutos tendremos 0,7[A]₀. Reformulando la ecuación de primer orden usando teoría de logaritmos, tenemos lo siguiente:

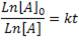
Reemplazando los valores dados, obtenemos:

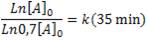
Eliminando [A]₀, llegamos a que:

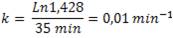
Ahora, usando nuevamente nuestra ecuación, podemos determinar qué concentración de A queda luego de 4 horas:

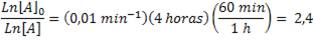
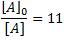
Por tanto, la fracción que queda sin reaccionar la determinamos invirtiendo el cociente anterior:

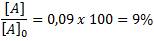
Quiere decir que, luego de cuatro horas, queda un 9% del reactivo inicial.

REACCIONES DE SEGUNDO ORDEN

Para una reacción genérica de segundo orden:  A →  B, la ley de velocidad será: v = k[A]²

o, lo que es lo mismo:

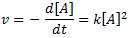
Resolviendo esta ecuación diferencial, llegamos a la expresión:

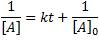
y las unidades de la constante de velocidad, en el caso de reacciones de segundo orden, es: M^-1t^-1

Si graficamos la inversa de la concentración vs. el tiempo, obtenemos una recta, pero en esta ocasión con pendiente positiva:

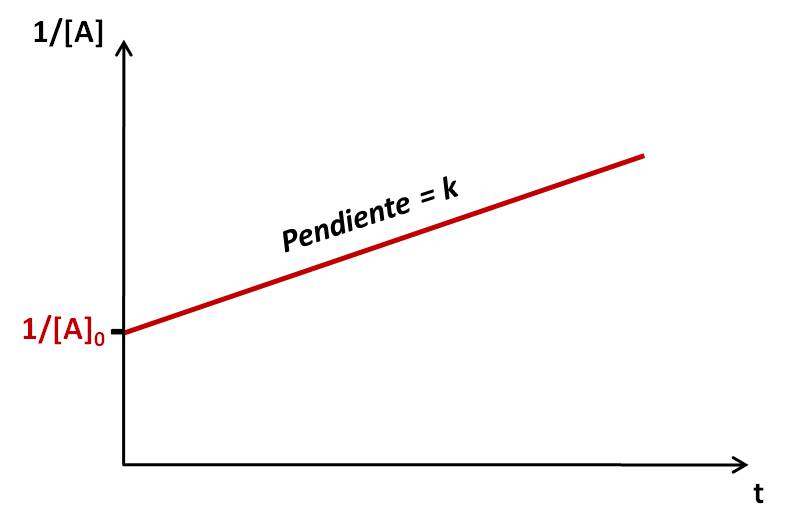
Observa que la pendiente es positiva: estamos graficando la inversa de la concentración. Por tanto, conforme avanza la reacción (y hay menos reactivo), la inversa de la concentración aumenta.
 

TIEMPO DE VIDA MEDIA

Se denomina tiempo de vida media al tiempo que transcurre para que la concentración de un reactivo disminuya a la mitad. Se denota por t_1/2. Eso quiere decir que es el tiempo que transcurre para que [A] = [A]₀/2.

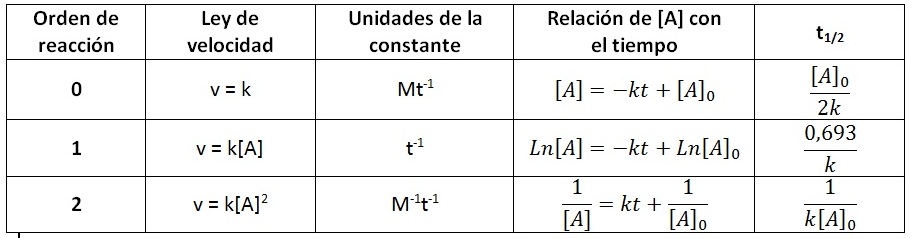
La expresión para la vida media depende del orden de la reacción, según la siguiente tabla:

Observa que el cálculo del tiempo de vida media depende de la concentración inicial y/o de la constante de velocidad. Asimismo, comprueba que las unidades del tiempo de vida media dependen de las unidades del tiempo que contiene la constante de velocidad.

IMPORTANTE No debe entenderse como que en dos tiempos de vida media se termina la reacción: más bien, en un segundo tiempo de vida media (2t1/2) la concentración disminuye a la mitad con respecto al período anterior. Es decir, la concentración del reactivo después de dos tiempos de vida media, será de [A]0/4.

Analicemos la siguiente reacción, que representa la descomposición del pentóxido de nitrógeno disuelto en un solvente apropiado:

2 N₂O_5(sol) →   4 NO_2(g)  +  O_2(g)

La reacción es de primer orden. Si graficamos la concentración de N₂O₅ con respecto al tiempo, obtenemos lo siguiente:

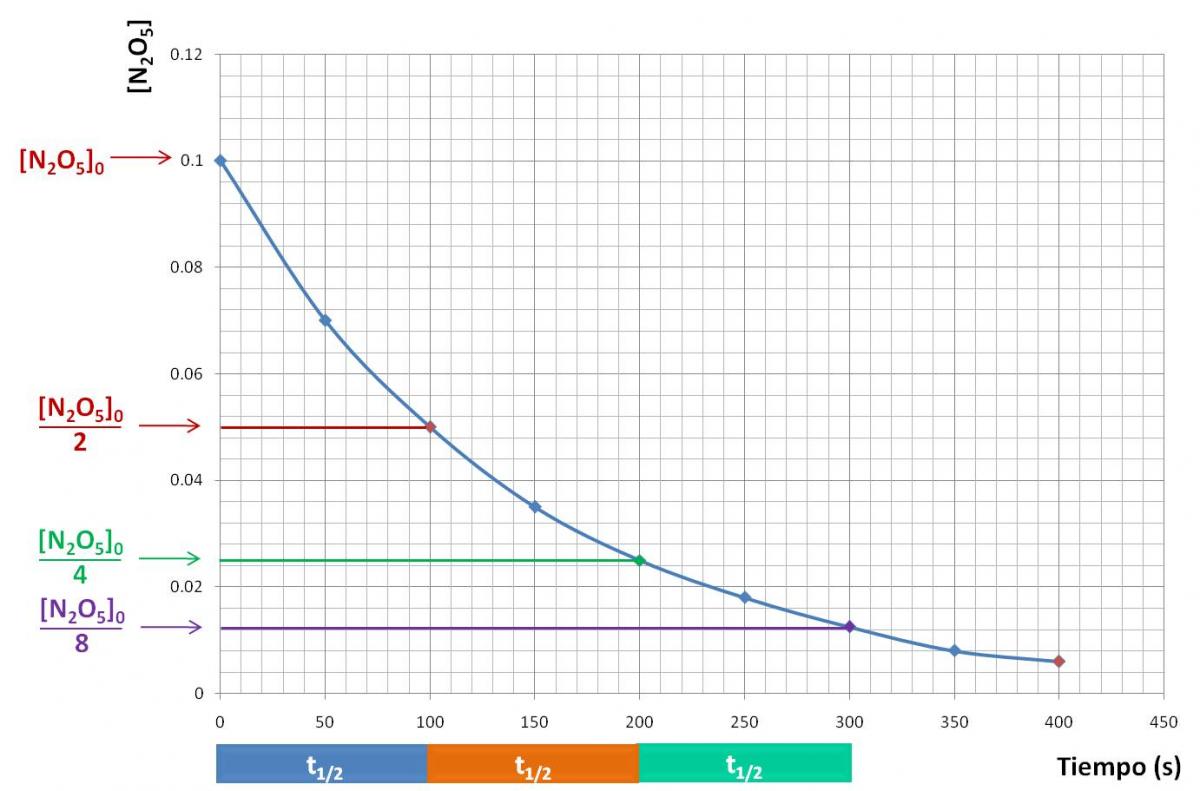
Podemos observar los intervalos correspondientes a los tres primeros tiempos de vida media. Observa que después del primer tiempo de vida media, la concentración de N₂O₅ disminuyó a la mitad de la inicial, es decir, cambió de 0,1 M a 0,05 M. Luego de otro tiempo de vida media, la concentración cayó a la mitad, con respecto al estado anterior: de 0,05 M a 0,025 M (la cuarta parte de la inicial). Por tanto, podemos concluir que el tiempo que transcurre para que la concentración cambie de 0,1 M a 0,05 M es exactamente el mismo que el que trascurrirá para que la concentración cambien de 0,02 M a 0,01 M.

Observación Si analizas el gráfico anterior podrás comprobar que la reacción no es de orden cero: la gráfica obtenida no es una recta. La gráfica de concentración vs tiempo sale recta sólo si la reacción es de orden cero.

CUADRO RESUMEN DE REACCIONES QUÍMICAS

INTERESANTE Seguro has escuchado el uso del carbono-14 como técnica para determinar la antigüedad de restos fósiles. Recuerda que el carbono-14 no es otra cosa que un isótopo del carbono, con número de masa 14: 14C. Este isótopo se descompone en nitrógeno 14N siguiendo una cinética de primer orden. Conociendo el valor de la constante de velocidad y las concentraciones iniciales y finales de 14C en un organismo, podremos saber el tiempo que ha transcurrido para que ocurra ese proceso y, consecuentemente, su antigüedad. Revisa el siguiente enlace interactivo para conocer más sobre el uso de 14C: http://www.andaluciainvestiga.com/espanol/cienciaAnimada/sites/carbono/carbono.htm