Cuando compramos carne, quesos o fruta en el supermercado, de inmediato las ponemos en la refrigeradora. ¿Por qué? simplemente porque estos alimentos se descomponen: si dejamos un queso sobre la mesa de la cocina durante dos días, lo encontraremos totalmente malogrado. Sin embargo, el proceso de descomposición (que es, de manera resumida, una reacción química) es más lento si los alimentos se guardan a menor temperatura.

Por tanto, podemos decir que la velocidad de una reacción es menor si la temperatura es menor, o en otras palabras: la velocidad de una reacción se incrementa con la temperatura.

Analiza el siguiente vídeo para confirmar esta observación:

TEORÍA DE LAS COLISIONES

Las reacciones químicas ocurren, como lo vimos en el tema “tipos de reacción”, mediante la colisión efectiva de los reactivos para formar productos. Analicemos el caso siguiente, de la reacción en la que A y B reaccionan para dar el producto AB:

A + B →  AB        v = k[A][B]

De la ley de velocidad, podemos observar que la reacción es de segundo orden: depende de las concentraciones de ambos reactivos. Consideremos un caso en el que tenemos dos moles de A y una mol de B: cada mol de A tiene un 50% de posibilidades de chocar con B y formar el producto determinado.

Sin embargo, si incrementamos la cantidad de B al doble (dos moles en lugar de una), la probabilidad de choque entre A y B se duplica: por tanto, la velocidad aumenta al doble.

Por tanto, nuestra primera conclusión en función de la teoría de las colisiones es la que ya conocíamos de la ley de velocidad y el método de velocidades iniciales: al incrementar la concentración de los reactivos, la velocidad de la reacción aumenta.

Por otro lado, pensemos ahora cómo interviene la temperatura en las moléculas: si aumentamos la temperatura, las moléculas poseerán mayor energía cinética y, consecuentemente, se moverán más rápido. Así, la posibilidad de chocar con otra molécula aumenta notablemente. Por tanto, podemos establecer que un aumento de la temperatura produce, necesariamente, un aumento de la velocidad de la reacción.

ENERGÍA DE ACTIVACIÓN

Hemos visto que para que una reacción ocurra, las moléculas de los reactivos deben chocar entre sí. Esto requiere una energía mínima imprescindible, la cual es necesaria para que se inicie la reacción. Esta mínima energía que se necesita se denomina energía de activación (E_a).

Si el sistema (formado inicialmente por los reactivos) no tiene una energía superior a la de la energía de activación, lo único que se tendrá es una mezcla de los reactivos. La reacción ocurre sólo si se alcanza esta mínima energía. Muchas reacciones ocurren a temperatura ambiente, es decir, la energía de activación es baja y, por tanto, el calor ganado del entorno es suficiente para que se inicie. Sin embargo, otras reacciones sólo ocurren al calentar los reactivos: tienen una energía de activación mayor.

La energía de activación suele representarse en un perfil de energía, es decir, un diagrama de energía vs el avance de la reacción. Consideremos la siguiente reacción exotérmica:

AB  +  C  →   A  +  BC         ΔH°< 0

El perfil de energía sería algo así como el mostrado a continuación:

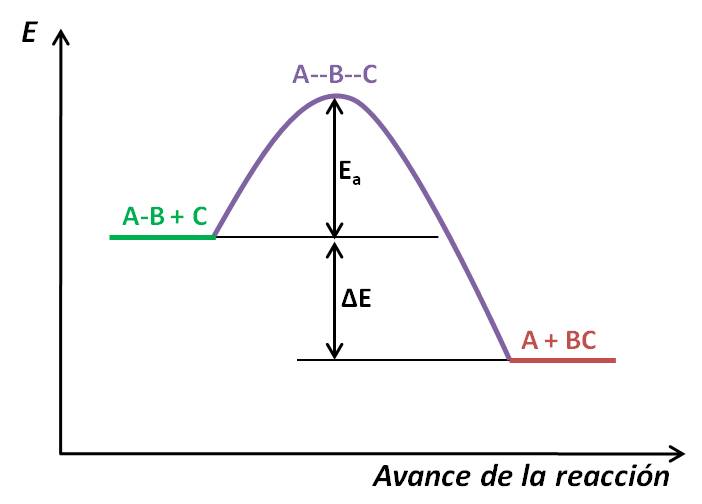
Este perfil muestra, cualitativamente, los cambios de energía a medida que los reactivos se transforman en producto. Al inicio de la reacción tenemos las sustancias AB y C (en verde), los cuales tienen, al inicio, una determinada energía. Para que estas sustancias reaccionen, deben chocar y formar un complejo activado (llamado también estado de transición), representado en morado: en él se aprecia que el enlace entre A y B se ha debilitado, mientras el enlace B-C empieza a formarse. La energía necesaria para alcanzar este complejo activado es la energía de activación (E_a). Una vez alcanzado este punto, se forman los productos (denotados en rojo). Observa que los productos se encuentran a una menor energía que los reactivos: esto quiere decir que los productos son más estables que los reactivos. Esto se da cuando la reacción es exotérmica.

IMPORTANTE La velocidad de una reacción dependerá de la magnitud de la energía de activación (Ea): una mayor Ea implica que la reacción es más lenta, ya que los reactivos tienen que ganar más energía para poder transformarse en productos. En consecuencia, al comparar dos reacciones: a mayor Ea, menor velocidad.

¿Qué pasaría si tenemos una reacción endotérmica? El perfil de reacción sería similar al anterior, pero con la diferencia de la posición de los productos con respecto a los reactivos: en una reacción endotérmica, los productos son menos estables que los reactivos (por ello se requiere calor) y se encontrarán más arriba en el perfil. A continuación un ejemplo:

Del diagrama, podemos deducir que el perfil mostrado es para la siguiente reacción:

DE  +  F   →   D  +  EF

Asimismo, observamos que los productos (en rojo) están a una energía mayor que los productos. Por tanto la reacción es endotérmica (ΔH°>0).

Observaciones Recuerda que el signo de ΔH° no interviene en la magnitud de la energía de activación: sólo afecta la posición relativa de los productos con respecto a los reactivos en el perfil de energía. Ten en cuenta que los perfiles de energía son cualitativos: no es necesario indicar valores, pero sí tener clara la posición relativa de los reactivos y productos en el mismo.

Ejemplo 2.3. Analiza los siguientes perfiles de energía para las reacciones “a” y “b”: ¿Qué podrías decir sobre las reacciones “a” y “b”: son exotérmicas o endotérmicas? ¿Qué reacción es más rápida: “a” o “b”?

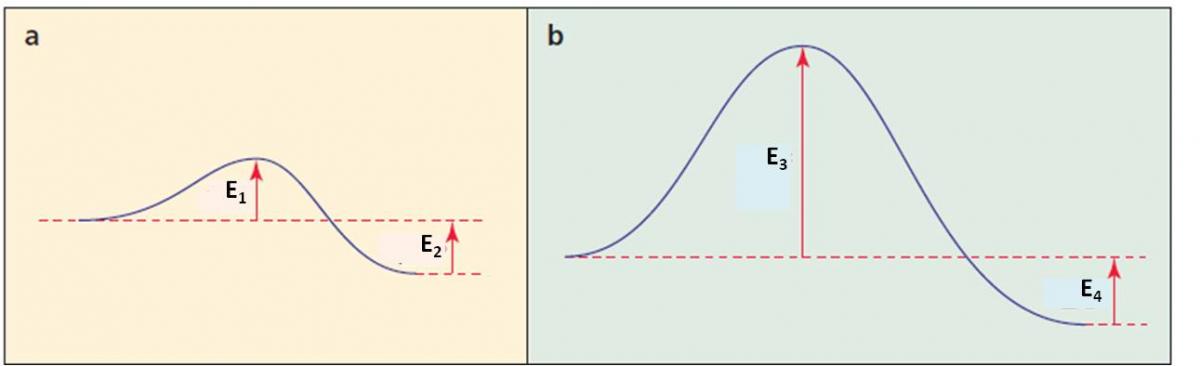
Para saber si las reacciones son endotérmicas o exotérmicas debemos fijarnos en la posición de los productos con respecto a los reactivos: en ambos casos, el final de la curva indica la posición de los productos, y en ambos casos, éstos están a menor energía que los reactivos. Por tanto, ambas reacciones son exotérmicas.

Para saber cuál reacción es más rápida, debemos comparar la energía de activación. En el caso de la reacción “a”, está dada por E₁. En el caso de la reacción “b”, está dada por E₃. Se puede apreciar que E₁ es menor que E₃, por tanto, la reacción “a” tiene una energía de activación menor y, consecuentemente, es más rápida.

ECUACIÓN DE ARRHENIUS

Svante Arrhenius, un científico sueco del siglo 19, estudió la dependencia de la constante de la velocidad de una reacción con la temperatura, al observar que la velocidad de una reacción aumentaba al aumentar la temperatura.

Svante Arrhenius. Tomado de: “biografías de científicos y científicas” (http://www.educared.org/global/anavegar5/Podium/images/C/2026/biografies.htm)

La ecuación de Arrhenius relaciona la constante de velocidad (k) con la temperatura:

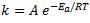
Donde:

Ea = energía de activación de la reacción (J/mol)
R = Constante de los gases: 8,314 J/mol.K
T = Temperatura (en K)
e = Base de los logaritmos naturales
A = Factor de frecuencia (Número que representa el número de colisiones)

Observa que tanto A, Ea y R son valores constantes para una determinada reacción. Si analizamos la ecuación, podemos ver que al aumentar la temperatura, el valor de la constante se incrementa.

Podemos expresar la ecuación de Arrhenius de una manera más clara al aplicar logaritmo natural a ambos lados de la ecuación:

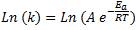
Que es igual a:

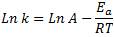
Y si la expresamos de la siguiente forma, obtendremos la ecuación de una recta:

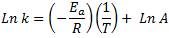
Así, si graficamos “Ln k” en el eje “y” vs la inversa de la temperatura "1/T" en el eje “x”, obtendremos una recta, cuya pendiente es “–Ea/R” y el punto de corte del eje “y” se corresponde con el valor de Ln A. Esta ecuación es útil para determinar gráficamente la energía de activación de una reacción.

Ejemplo 2.4. La descomposición del silano (SiH4) tiene los  valores de constantes de velocidad a distintas temperaturas que se muestran en la tabla. Determinar la energía de activación de la reacción. SiH4(g)  →   Si(s)  +  2 H2(g)

Utilicemos el método gráfico. Para ello, debemos representar el “Ln k” vs “1/T”, y obtendremos una recta. La pendiente de tal recta será “-E_a/R” y, de ella, podremos obtener el valor pedido.

En efecto:

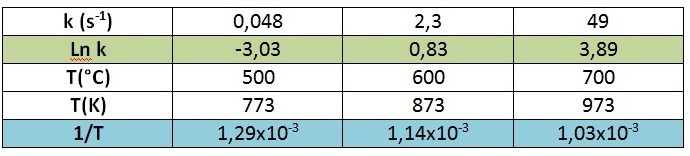
Graficando “Ln k” vs “1/T”:

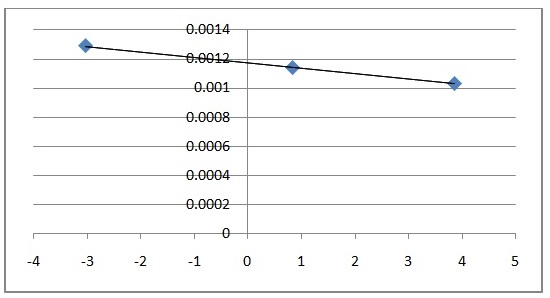
Podemos calcular la pendiente entre dos puntos consecutivos según: m = ?y/?x

Calculando el promedio de las pendientes, obtenemos: m = - 26775,75 = - E_a/R

Reemplazando el valor de R, obtenemos que Ea = 222,6 kJ/mol.

La ecuación de Arrhenius es útil también para determinar el valor de la constante de velocidad a otra temperatura. Para ello, se sustituye en la ecuación de Arrhenius los valores k₁ y T₁ y k₂ y T₂ para dos casos hipotéticos, obteniéndose la siguiente ecuación:

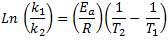
Esta ecuación nos permite calcular la constante de velocidad de una misma reacción a otra temperatura, conociendo el valor de la constante de velocidad a cierta temperatura, y el valor de la energía de activación.

Ejemplo 2.5. El disulfuro de carbono (CS2) se forma a partir de metano según la siguiente reacción en fase gaseosa: CH4(g)  +  2 S2(g) →  CS2(g)  +  2 H2S(g) La constante de velocidad de esta reacción es de 1,1 M-1s-1 a 823 K. Si la energía de activación es de 120 kJ/mol, estimar el valor de la constante de velocidad a 900 K.

Asignemos valores a cada una de las expresiones de la ecuación:

k₁ = 1,1M^-1s^-1
T₁ = 823 K
k₂ = ¿?
T₂ = 900 K
E_a = 120000 J/mol

Reemplazamos los valores en la ecuación:

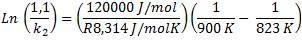
Aplicando exponencial a ambos lados, logramos despejar k₂ = 4,93 M^-1s^-1

Observación No olvidemos que la constante a otra temperatura tendrá unidades,idénticas a las que utilizamos como dato para calcularla. Estas unidades no se toman en cuenta durante el cálculo, ya que no podemos aplicar logaritmo a las unidades, pero si debemos tenerlas en cuenta en nuestra respuesta final.